文章目录
- 堆排序
- 向上调整建堆
- 向下调整建堆
- 堆排序调整过程
- Top-K问题
堆排序
排升序要建大堆,排降序要建小堆(这里以排升序为例)
排序思想:
1.首先将待排序的n个数建成大堆(此时堆顶是n个数里最大的).
2.将堆顶的值与和最后一个数交换,此时最大的值在n的位置不用管,排序剩下n-1个数(此时根除外左子树和右子树各自依旧是大堆)
3.然后向下调整,选出n-1个数里最大的值,再和n-1个数的最后一个值交换,此时n-1位置放的是第二大的值
4.然后再排剩下的n-2个数,重复就能得到这升序。
以这个数组a[] = { 4,6,2,1,5,8,2,9 }为例
这里建堆有两种方法:
向上调整建堆
1.把数组的第一个数当成一个堆,然后往后插入值再向上调整

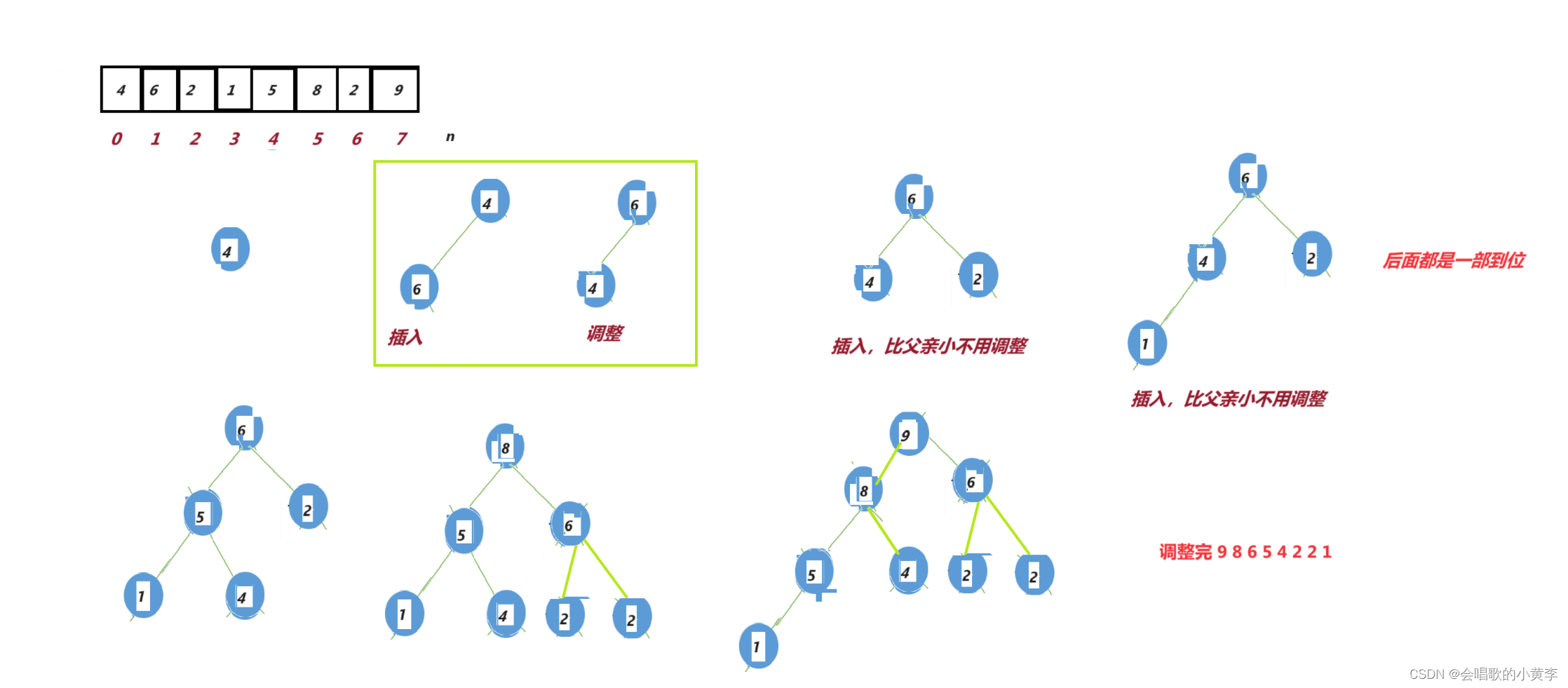
这种建堆的时间复杂度为O(NlogN)

向下调整建堆
2.找到最后一个数的位置,然后找到它的父亲,再调整。

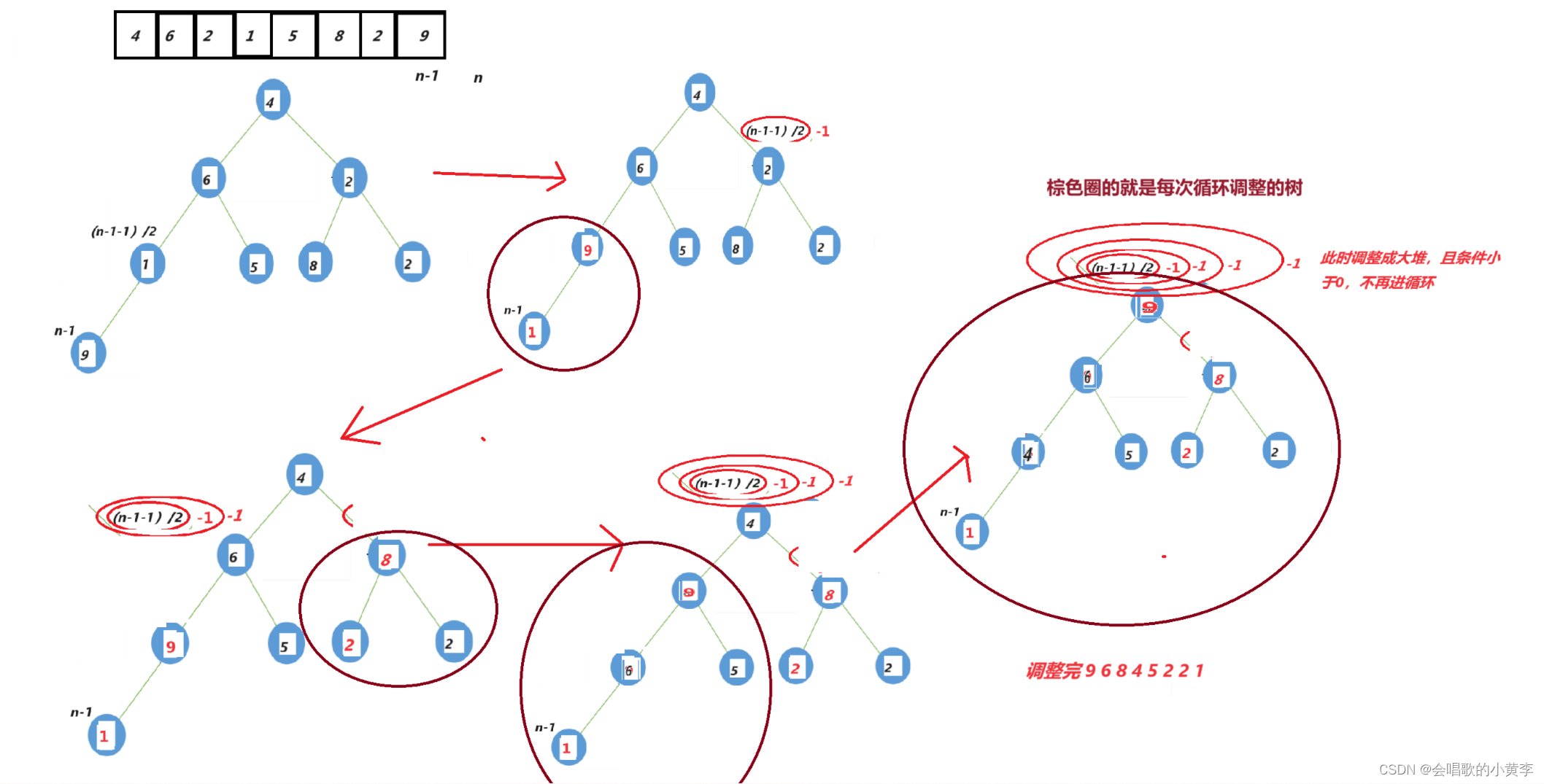
这种方法的建堆时间复杂度为O(N)
我们建堆肯定首选时间复杂度低的咯,所以我们一般建堆都是用向下调整建堆。
//这里是排升序,所以要建大堆
//交换函数
void Swap(HDataType* p1, HDataType* p2)
{
HDataType tmp = *p1;
*p1 = *p2;
*p2 = tmp;
}
//向下调整算法
void AdjustDown(HDataType* a, int size, int parent)
{
//假设左孩子大
int child = parent * 2 + 1;
while (child < size)
{
if (child + 1 < size && a[child + 1] > a[child])//确保有右孩子,如果错了,更新到右边
{
++child;
}
if (a[child] > a[parent])
{
Swap(&a[child], &a[parent]);
parent = child;
child = child * 2 + 1;
}
else
{
break;
}
}
}
//向上调整算法
void AdjustUp(HDataType* a, int child)
{
int parent = (child - 1) / 2;
while (child > 0)
{
if (a[child] > a[parent])
{
Swap(&a[parent], &a[child]);
child = parent;
parent = (parent - 1) / 2;
}
else
{
break;
}
}
}
void Heapsort(HDataType* a, int n)
{
建堆N*logN
//for (int i = 1; i < n; i++)
//{
// AdjustUp(a, i);
//}
//建堆N
for (int i = (n - 1 - 1) / 2; i >= 0; i--)
{
AdjustDown(a, n, i);
}
//排序N*logN
int end = n - 1;
while (end > 0)
{
Swap(&a[0], &a[end]);
AdjustDown(a, end, 0);
--end;
}
}
int main()
{
int a[] = { 4,6,2,1,5,8,2,9 };
int sz = sizeof(a) / sizeof(a[0]);
Heapsort(a, sz);
for (int i = 0; i < sz; i++)
{
printf("%d ", a[i]);
}
printf("\n");
return 0;
}
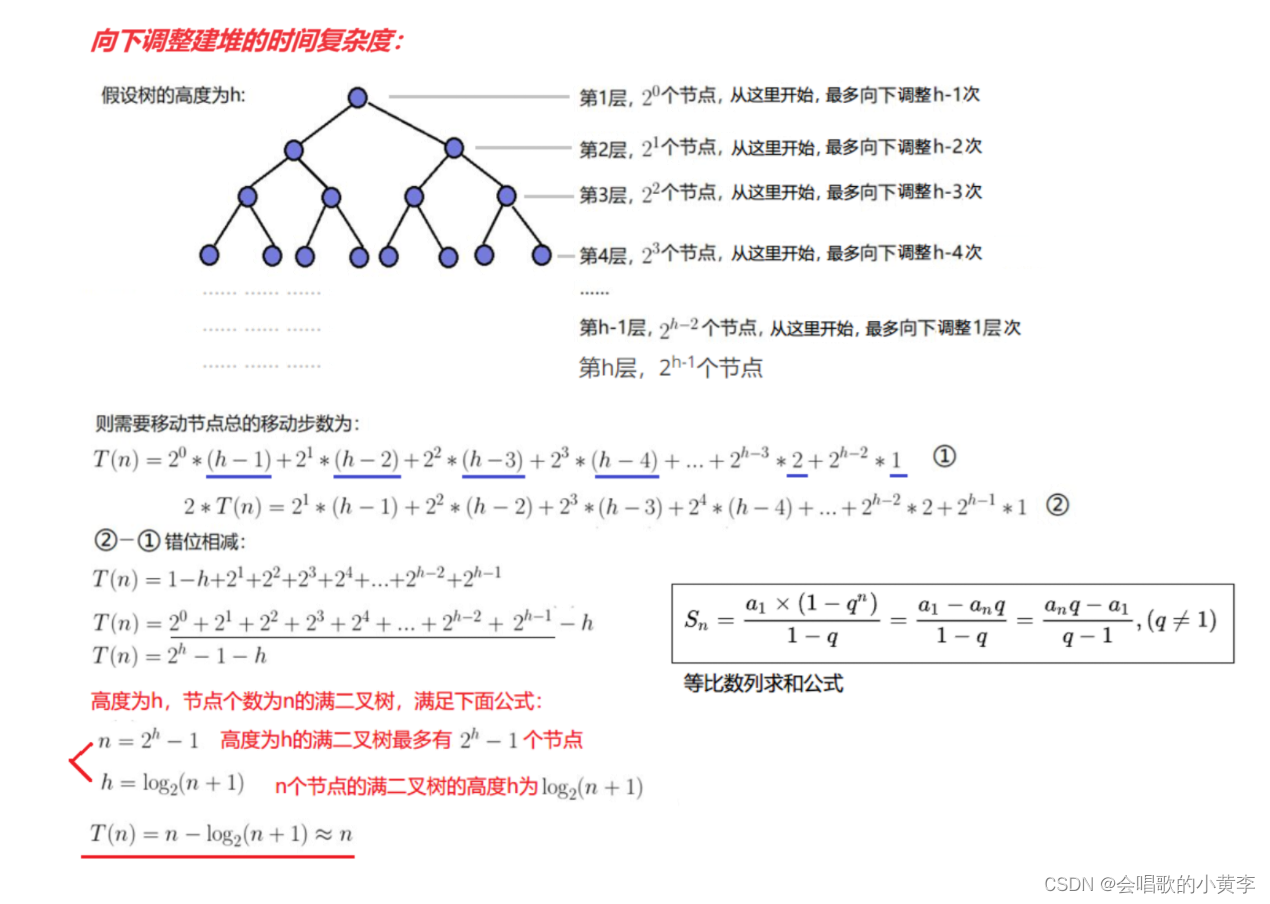
堆排序调整过程
当在h层时:有2^h-1个元素, 从最顶上到最底下需要走最多h-1次
从最顶上到最底下 ,所有元素需要花费的次数为 2^h-1 * (h-1)
当在h - 1层时:有2^h-2个元素, 从最顶上到最底下需要走最多h-2次
从最顶上到最底下 ,所有元素需要花费的次数为 2^h-2 * (h-2)
最终需要花费的时间就是与上面的向上调整法的结果一样,时间复杂度为O(NlogN)。
堆排序筛选法建堆和堆调整过程结合到一起,时间复杂度是O(N)+O(NlogN),进一步堆排序时间复杂度为O(NlogN)量级。
Top-K问题
TopK问题是一种常见的算法问题,要求从一组元素中找到最大或最小的K个元素。这类问题在日常生活中也经常遇到,例如排名、销量、评分等。TopK问题可以通过排序的方式解决,但是效率较低,一种更高效的方法是利用堆这种数据结构,每次堆顶要么是最大或者最小的元素。这种方法的时间复杂度是N*logK,而且不需要在内存中读入全部的元素,适用于大数据集。
我们举个例:从数据个数为9的数组a[] = { 4,3,7,9,1,5,8,2,8 };中找到前k = 3个最大的数。
第一种方法:刚刚学的堆排序就派上用场了,但是时间复杂度为O(NlogN)
如果数据量非常大,排序就不太可取了(可能数据都不能一下子全部加载到内存中)
第二种方法:就是建N个大小的堆,建N个数的堆为O(N),获取堆顶元素,删除掉堆顶元素为O(logN),上述操作重复 k 次,所以时间复杂度为O(N+klogN)。
如果 N 是 10 亿数,内存中放不下,是放在文件中的,前面两个方法都不能用了。
第三种方法:建k个大小的堆,将剩下的N-k个数与堆顶进行比较,比堆顶大则替换,再进行向下调整,让其再成堆,重复以上动作即可。时间复杂度:O(k + (N-K)logK)。当 N 远大于 K 时,则为O(NlogK)。
结合文件操作演示
//交换函数
void Swap(HDataType* p1, HDataType* p2)
{
HDataType tmp = *p1;
*p1 = *p2;
*p2 = tmp;
}
//向下调整算法
void AdjustDown(HDataType* a, int size, int parent)
{
//假设左孩子小
int child = parent * 2 + 1;
while (child < size)
{
if (child + 1 < size && a[child + 1] < a[child])//确保有右孩子,如果错了,更新到右边
{
++child;
}
if (a[child] < a[parent])
{
Swap(&a[child], &a[parent]);
parent = child;
child = child * 2 + 1;
}
else
{
break;
}
}
}
//向上调整算法
void AdjustUp(HDataType* a, int child)
{
int parent = (child - 1) / 2;
while (child > 0)
{
if (a[child] < a[parent])
{
Swap(&a[parent], &a[child]);
child = parent;
parent = (parent - 1) / 2;
}
else
{
break;
}
}
}
void CreateNData()
{
int n = 10000000;
srand(time(0));
const char* file = "data.txt";
FILE* fin = fopen(file, "w");
if (fin == NULL)
{
perror("fopen fail");
return;
}
for (int i = 0; i < n; i++)
{
int x = (rand() + i) % 10000000;
fprintf(fin, "%d\n", x);
}
fclose(fin);
}
void PrintTopK(const char* file, int k)
{
FILE* fout = fopen(file, "r");
if (fout == NULL)
{
perror("fopen fail");
return;
}
//建一个k个数的小堆
int* minheap = (int*)malloc(sizeof(int) * k);
if (minheap == NULL)
{
perror("malloc fail");
return;
}
//读取前k个,建小堆
for (int i = 0; i < k; i++)
{
fscanf(fout, "%d", &minheap[i]);
AdjustUp(minheap, i);
}
int x = 0;
while (fscanf(fout, "%d", &x) != EOF)
{
if (x > minheap[0])
{
minheap[0] = x;
AdjustDown(minheap, k, 0);
}
}
for (int i = 0; i < k; i++)
{
printf("%d ", minheap[i]);
}
printf("\n");
fclose(fout);
}
int main()
{
CreateNData();
PrintTopK("data.txt", 5);
return 0;
}





![【CTF Web】NSSCTF 3863 [LitCTF 2023]导弹迷踪 Writeup(JS分析+源码泄漏+信息收集)](https://img-blog.csdnimg.cn/direct/17af0635dd36449a9c751f2729d4867a.png)


![[C++核心编程-08]----C++类和对象之运算符重载](https://img-blog.csdnimg.cn/direct/730eea47b2ad4e208f5b00f0a28ce6cb.png)